Measuring flowrate and creating models

I was interessted in the flow characteristics of coffee in my Gaggia Classic machine. Obviously, this depends on many variables, namely: pressure, coarseness settings of grinder, type of beans, age of beans, humidity of beans, type of portafilter, grams of coffee, filling in the portafilter, pressure while tamping, homogenity of ground coffee, ...

You can probably extend this list forever but we won't get anywhere if we try to calculate with all these variables.

Some basic test I did was the following: Put 19g of coffee (Black Ape from Quijote Coffee in Hamburg) ground at the same setting (in my case 1E on the Mahlkönig Vario II - which will not help you anything because the settings are different on every machine!) into a VST 20g portafilter (at least this one is compareable). Then take two shots and measure the wheight of coffee in the cup.

But there is one problem: I do not have a scale with a logging output, so I had to improvise here. I filmed the scale while brewing and then noted the scale readings for each second using kdenlive.

The raw file can be downloaded here: raw.txt.

The readings are not super accurate and my scale is also not the best (Sorry, no Brewista :( ...) but for what I try to do, it is fine.

Putting them into R for some plotting, we get fancy graphs.

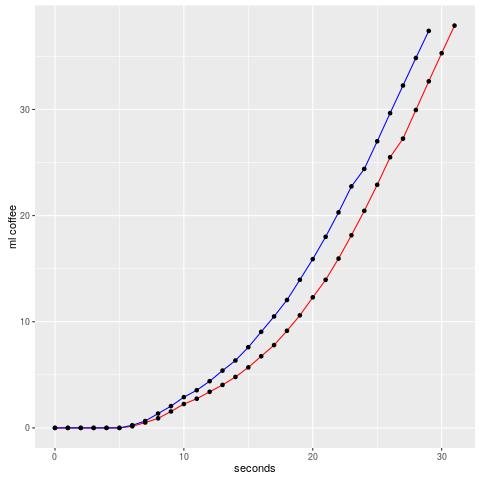
brewing the coffee. red: first brew, blue: second brew

First of all, we can see that the curve looks quite identical, but the second brew (blue curve) is shifted to the left - which means it ended earlier. I aimed for a yield of about 2, in this case 38g and shut off the machine as the cup weight was reaching this value.

Now the really interessting part is, what was the flowrate? We can easily obtain this value by differentiation of the values.

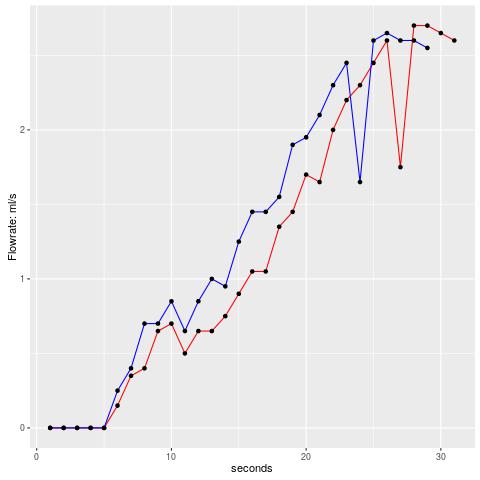
Flowrate the coffee. red: first brew, blue: second brew

One very interessting thing is the drop near the end. It occours in both brews and is very likely an aliasing artefact from the measurement process. I have to admit, that reading the values from the video is not so easy and a higher sampling rate would probably help. There are two limiting factors here: the sampling rate of the scale (i think it is about 500ms) and my sampling rate (1s). It is very likely possible that both sampling rates interfered in such a way, that i read an old value. Interesstingly this happend at the same spots (there are some more in the curve, as you can see).

What is the result now? As you can see, there is an continously rise of the flow rate. The maximum flow rate is limited by the pump (looking at the datasheet, you can find a value of about 5ml/s at 8 bars, which is my pump pressure while brewing) and probably not reached after 30s. The resistance of the coffee is probaly too high.

So one experiment could be to brew for a longer time, for example for one minute and check when the change in flowrate is constant. It would be interessting if the flow rate will be higher than our maximum value of 2.7 ml/s because we can see a stagnation in flowrate in the end. Maybe this is also an artefact...

Another thing we can do now, is to create a model which fits the brewing process. With such a model we could, in theory, calculate the brewing time to produce a certain yield. In the real world, this is of course much more complicated...

But a model can still be calculated. The real problem is the beginning of the brew. It starts quite slowly then increases rapidly. The first five seconds, there is now flow and thus the values are zero - which is especially hard to fit.

I tried with a quadratic model, which gives some nice fitting in the end but the beginning is not fitted correctly (the intersection with 0 is wrong).

But still, we try to find a model for the complete brewing process and probably will not model the start.

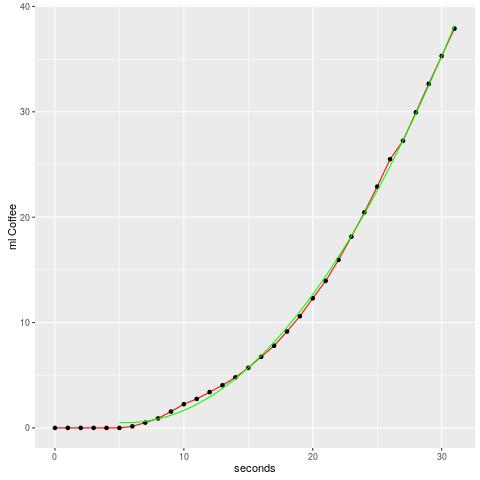
Prediction of Model for flow. red: first brew, green: model

The equation for this model was 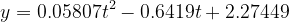y = 0.05807t^2 - 0.6419t + 2.27449 .

If you like, take a look at my unsorted R History file: .RHistory

This experiment also gives interessting insight into brewing to a specified yield. If you would like to have excactly 2 times the dose, you need to shut off the brewing at a specific point. But as you can see, the flowrate in the end of the brew is already 2.7 ml/s, so if you do not shut off the brew in time, you have a few mililiters more in the cup.

On the other hand, the variations in the brew are also in the order of some mililiters (see the shift in curve to the left), so controlling the brew in this direction is also difficult.

On machines, where you can control the pressure, those problems are circumvented by lowering the pressure in the end of the brew. Therefore the flow lowers too, thus aiming for a specific yield gets much easier.

To test the hypothesis, that the rate of flowrate will not change when the $t \gg 1$ , I took some old coffee I had lying around and put it into the portafilter. Then the same measurement method from above was used but for a longer time. In this case I took measurements for 58 seconds resulting in 237ml of coffee.

The coffee must be really old, because flow was from the beginning on (starting after 1,5s). But this was actually good, because now we can observe the behaviour of flow better. The pressure was quite constant at 8 bar, but I did not monitored it the whole time. The data can be downloaded here: raw_long.txt.

Volume and Flowrates can be seen in those two plots:

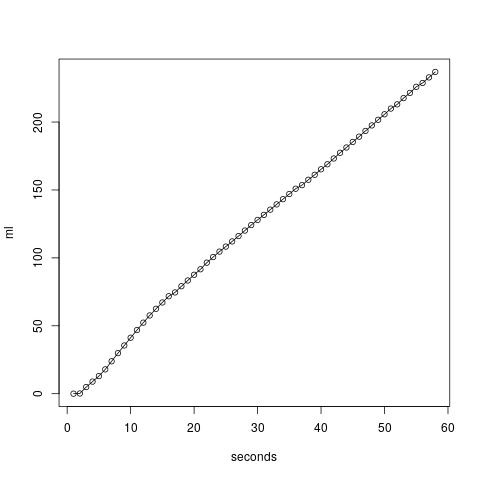
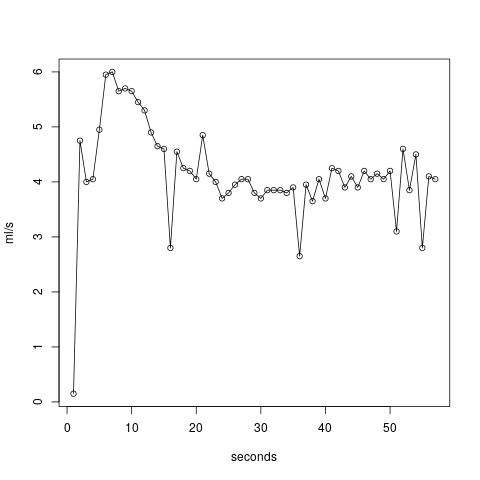
Volume over one minute Flowrate over one minute

Again, we have some aliasing artefacts... At the beginning the flow seems to be higher, maybe the pressure was also higher then. But the the flowrate becomes quite linear at about 4ml/s, which is actually close to the value from the datasheet. Beware that I have a membrane dampener installed and set my overpressure valve to about 9 bar, so maybe some flow is going back into the tank. If I had a second scale, I could also monitor that...

So what do we learn from this experiment? That our model of a quadratic function is probably wrong. Of course it is, because think about the implications: If the flow is really quadratic, this would mean an infinite increase in flow. Which is not what we see in real life: the maximum flowrate is limited by the pump. So a more real model would be to assume the flowrate to have some sigmoidal shape, e.g. 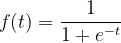$f(t) = \frac{1}{1 + e^{-t}}$ . 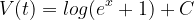If we integrate this, we get a formular for the volume: V(t) = log(e^x + 1) + C . This curve has a short rising time in the beginning and is then linear, which seems to be the case. In this measurement, this is not visible, because there is actually no increasing flow, but the flow is instantaneous at its peak. Consider the first measurement for the beginning and then the later curve for the end.

To actualy fit some curve, I would like to test this with good coffee and a scale which can log to the PC... Maybe I have to hack some cheap precision scale to output the weight as voltage, so I can log it with my multimeter (which has a serial port).