Because I had some hard hours to figure this one out (basically I mixed a lot of degree and radians and messed up several times with tan and sin), here is my solution. It may be a help for someone (or for me later...).
The quest was to find the angle of a line through a point lying on a circle, when this line is parallel to some line passing through another point on the circle.
So let's get this started:
Lets say, we got a point 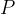 with the coordinates
with the coordinates 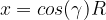 and
and 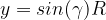 , thus they are on the circle with radius
, thus they are on the circle with radius 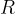 ,
centered at the origin.
,
centered at the origin.
Now, we construct a line through the circles' circumference at 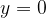 ,
thus we know it must pass through
,
thus we know it must pass through 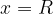 .
The line equation is then given by
.
The line equation is then given by 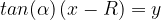 .
.
Now, we construct a parallel line to it (in direction of negative x) with distance 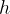 , which is given
by the line equation
, which is given
by the line equation 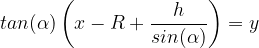 .
.
To find now the angle, we insert the point into the equation, as we require that the line
passes through this point:
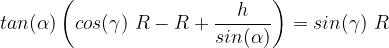 .
.
I tried to solve this by hand but the formular we get is quite complex (and I found it using wolframalpha, not by hand).
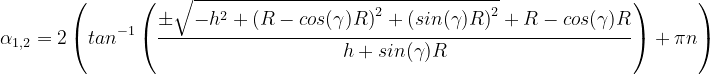
with 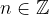 . But as we know, that the angle must be between
. But as we know, that the angle must be between 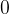 and
and 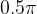 , we can just set
, we can just set 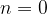 and remove that part.
and remove that part.
You might ask: why do you need something? Here is an example: lampe.scad I tried to arrange the rectangles in such a way, that they are rotated and touch each other. We can calculate now, that the angle (in this specific configuration) is about 57 degree.
Thank's to OpenSCAD, where you learn math the hard way ;)