the science of boiling eggs

← Rant: Java versions in Debian | Blog | fixing a hario scale →

There is a very interesting article in German on boiling eggs from one of the Science Busters Werner Gruber: Wie lange kocht man ein 3-Minuten Ei?.

This article gives an equation how long an egg must boil for a certain core temperature to reach:

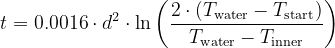
$t = 0.0016 \cdot d^2 \cdot \mathrm{ln}\left(\frac{2 \cdot(T_{\mathrm{water}} - T_{\mathrm{start}})}{T_{\mathrm{water}} - T_{\mathrm{inner}}}\right)$

For a soft-boiled egg, the value of 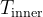$T_{\mathrm{inner}}$ should be above 61.5°C but below 65°C. The article specifies 62°C as the target but another page, which is citing this article gives 64°C as the target value. We use this higher value here.

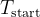As $T_{\mathrm{water}}$ can be set to 100°C and $T_{\mathrm{start}}$ can be assumed to be 4°C, if the egg comes from the freezer, the whole equation can also be written as:

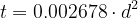
$t = 0.002678 \cdot d^2$

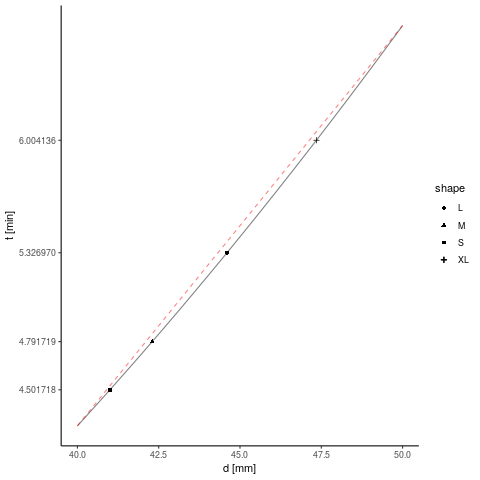
A normal egg has a minor diameter of about 41mm (S) to 49mm (XL). Plotting the function between these values, we can see, that the curve is almost linear in this region. The linear function can be calculated as:

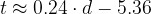
$t \approx 0.24 \cdot d - 5.36$

Thus, to have an "in the ballpark" figure for the boiling time, just take a quarter of the minor diameter and subtract 5 and a half minutes from the result and take the eggs out a little bit earlier ;)